Fractals

What are Fractals?

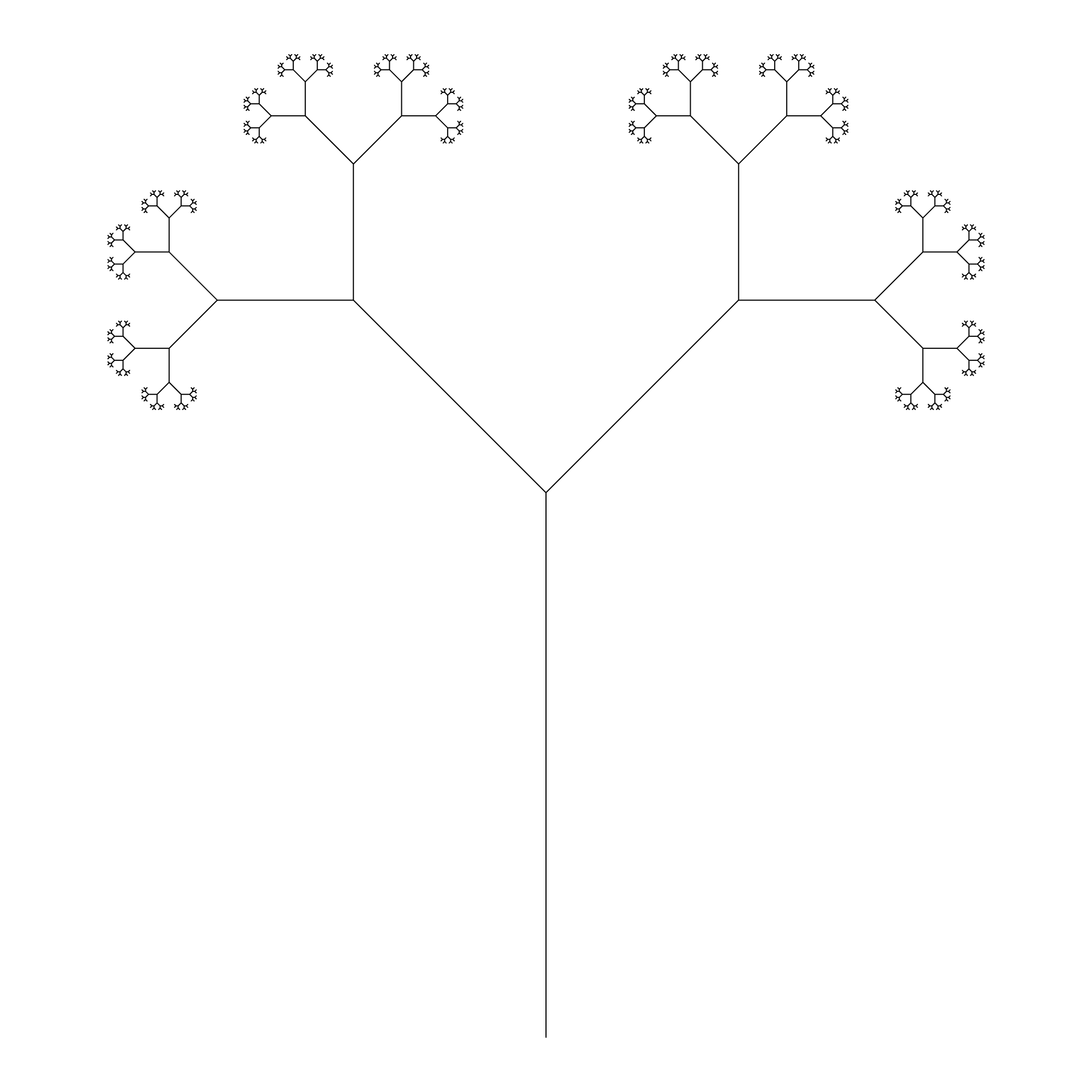
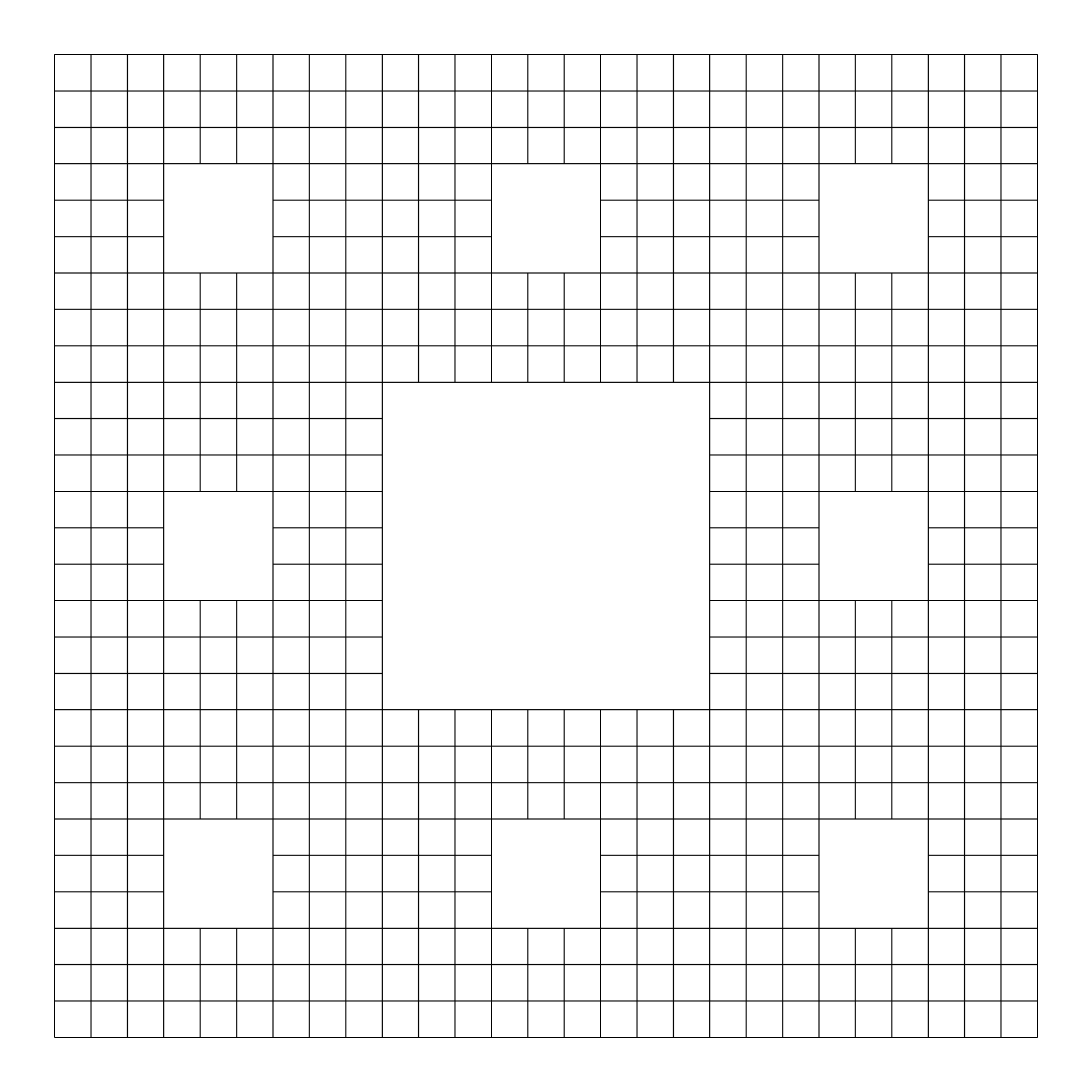
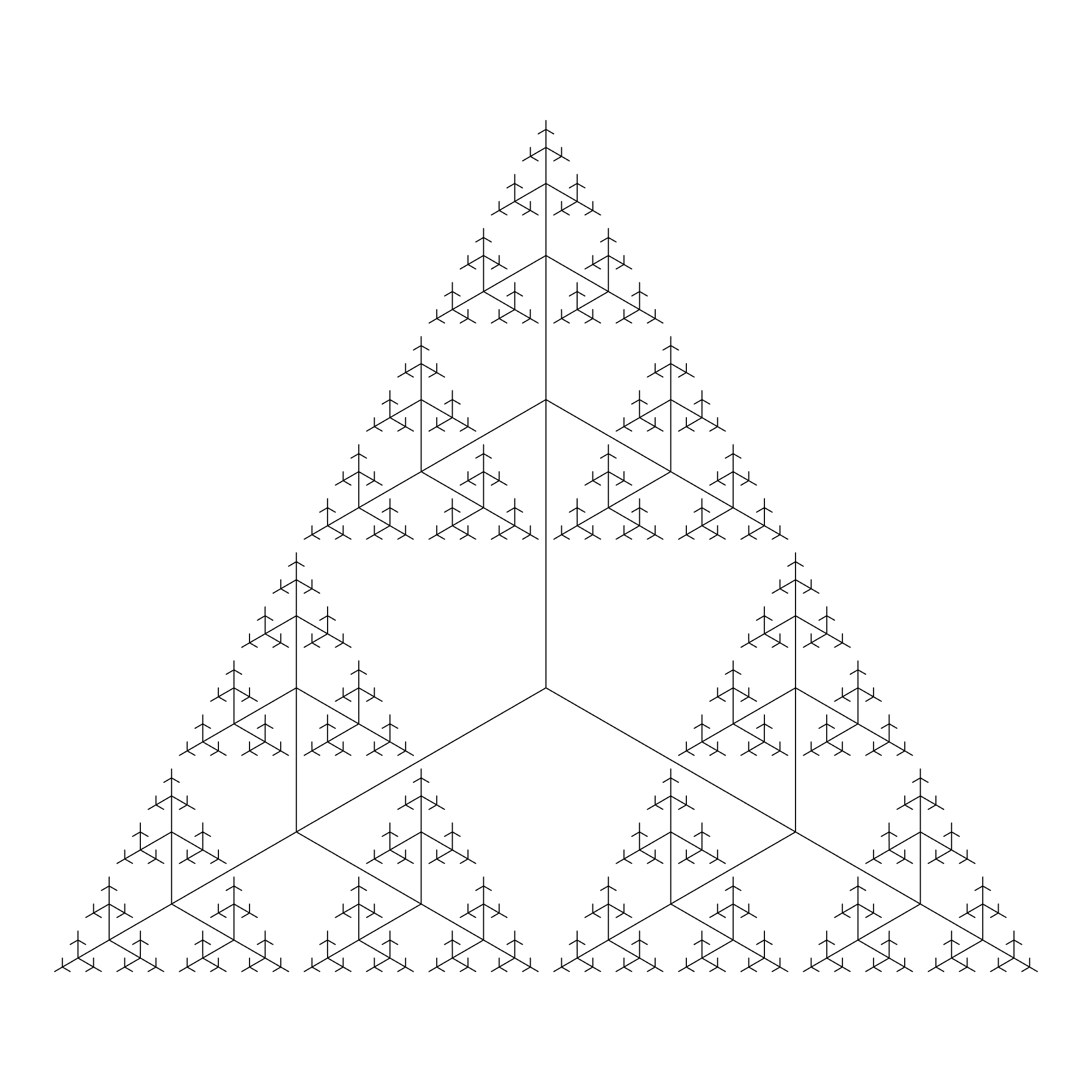
In mathematical terms, a fractal is a geometric shape that contains details at arbitrarily small scales, and thus has a fractal dimension, strictly greater than the topological dimension.

Many fractals appear similar at various scales in successive magnification. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry.

If this replication is exactly the same at every scale, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

Occurrences and Applications

As fractal geometry is a branch of measure theory in mathematics, it was developed to understand and measure natural phenomenon and objects with properties that have self-similarity and replicative properties.

If you look around yourself carefully you'll be able to observe fractals too. Want a hint, trees, waves, flames, flowers, snowflakes, etc.

With these new methods, we're able to look at the world in a different way, which lead us to develop better solutions for certain problems.

Want to know what real-world solutions use fractals, electronics, art, design, geology, mechanical systems, molecular biology, graphics, medicine, fashion, architecture, computation, etc.

Why I made this?

Amidst a summer, while drifting YouTube, I landed on a video by 3Blue1Brown about fractals and that captivated me and left me intrigued which led me into reading various articles, books, and watch some videos. In the end I decided to make something to draw them and here we are.

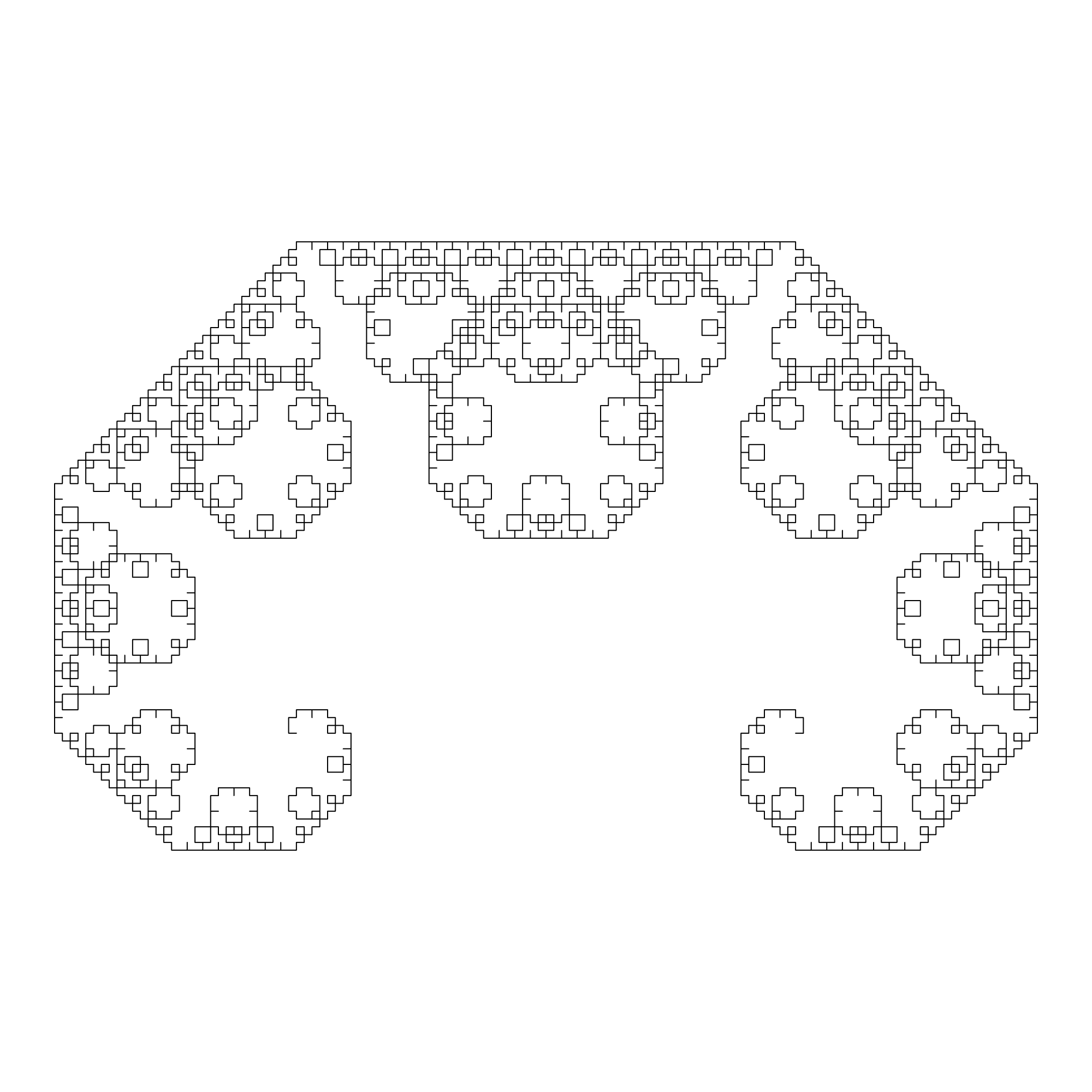
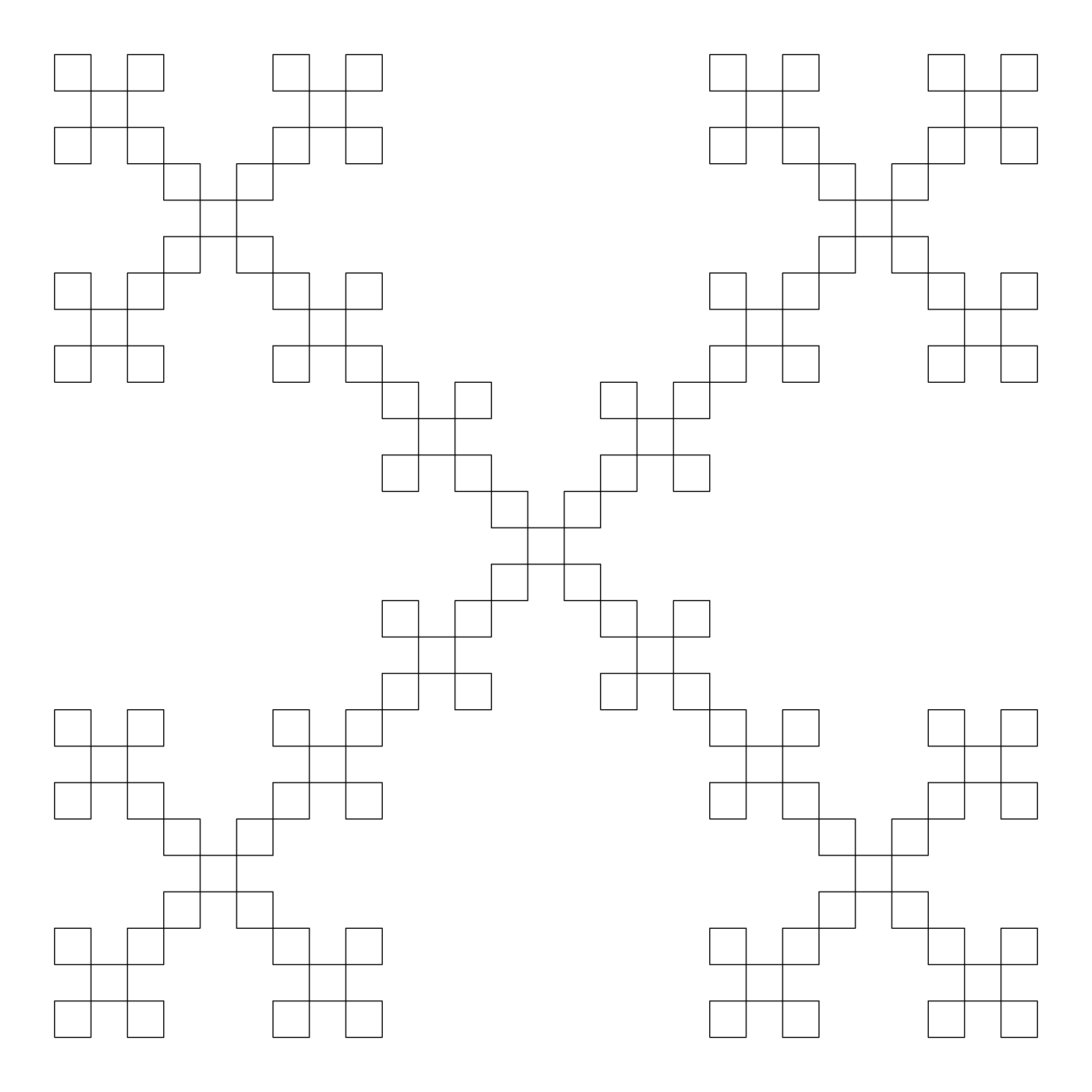
Below you can find some basic fractals that you can look at.